Book progress update

At the beginning of the summer, I set myself the goal to clear the 161 to-do notes from the draft of my book by the first of December, which meant doing about 1 a day.  I kept up for quite a while, but I am now a little behind schedule, with 48 to-do notes left, which would have me finishing on December 5, if I maintained one a day. The book is now 637 pages, with 315 images in 256 figures (many have subfigures).  I think I may be done adding figures, but the remaining to-do notes include adding a few pages of text (which may or may not increase the page count for the overall book, depending of how much white space there is at the end of the relevant chapters).

I was keeping pretty well to schedule over the summer, but I fell behind during the Santa Cruz Shakespeare trip to the Oregon Shakespeare Festival in Ashland. The trip was worth the time—I saw six plays: two very good (La Comedia of Errors and All’s Well That Ends Well), one well-acted but with a bit of a thin script (Mother Road), one well-acted but with awkward sets and strange direction that did not really work (Macbeth), one interesting but deliberately uncomfortable play (Between Two Knees), and one awful production (As You Like It) that failed in almost every way.  The original script for As You Like It is good, but the director managed to mangle it by rearranging speeches, assigning them to the wrong characters, cutting excessively, and generally making a hash of it. Gender roles were randomly reassigned, the wrestling match was played for laughs (like a video game), Touchstone was played very stiffly, and Jaques was changed from a melancholy character into a giddy one.  The costuming was also poor—I felt very sorry for the actors having to put up with such a poor interpretation of the play.

I’m on leave this quarter, so I don’t have to teach, go to meetings, or hold office hours, but I’m taking a physics course (PHYS 102, which is an introduction to quantum mechanics).  The homework for the physics class has been taking quite a bit of time, and I have been prioritizing it over the book writing. I brought my laptop with me on the Ashland trip, but I didn’t do any writing for the book—I finished the first homework for the physics class instead, as it was due the day after we came back.  Today I finished homework 3 for the physics class (due Monday), so I should work on the book this weekend.  Maybe I can get back on schedule? (Or maybe I’ll try mowing more of the back lawn—I’ve cleared about a quarter of it.  Creative Procrastination!)

I’ve also been wasting a lot of time reading news, humor, and a few subreddits on the internet—the physics class is only taking about 15 hours a week, so I can’t really blame the class for my being behind schedule on the book.

Lagrangian mechanics for linear electronics

This post is a continuation of Having trouble learning Lagrangian mechanics, looking at electronic systems rather than mechanical ones.  Again, this is not intended as a tutorial but a dump of my understanding, to clarify it in my own head, and to get corrections or suggestions from my readers, many of whom are far better at physics than me.

For electronics, I’ll use charge as my coordinate, with current $i = \dot q$ as its derivative with respect to time.  In all but the simplest circuits, there will be multiple charges or currents involved, which I’ll distinguish with subscripts.

Some notation:

• is the difference between kinetic and potential energy of the system.  The potential energy will be the energy stored in capacitors, , and the kinetic energy the energy in the inductors, .  (Note: that is only self-inductance.  If we have mutual inductance between two inductors, we need to use for the kinetic energy—I’m a bit confused by that, as we could have negative kinetic energy.  I rarely use inductors or transformers in my electronics, so I’ve not had to work out my confusion yet.)
• is the power dissipated by the resistors in the system: .
• is the vector input to the system needed to make the energy balance work out.  By using charge for each coordinate, the units here will be volts.

With this notation, the basic formula is

Let’s check the units:

• Potential energy: , which is indeed volts.
• Kinetic energy: , which is also volts.
• Dissipated power:, which is again volts (Ohm’s Law).

Now all we need to do is to figure out which  or has to be associated with each component of the system, and what voltages the correspond to.  I think that will be easiest if I have some specific circuits to work with.  Let’s start with a very simple one:

Simple RLC series circuit with a voltage source.

We can use a single coordinate, the charge on the capacitor, , so that the current flow is clockwise in the schematic. We get the Lagrangian The power dissipation is , and taking the derivatives gives us , which is the voltage for the voltage source.

For electronics modeling, we often want to look at the ratio of two different voltages in a system, for example, the output of a filter relative to the input to a filter. How do we set that up? Let’s look at a very simple low-pass RC filter:

The upper schematic shows the normal way to represent the low-pass filter. The lower schematic shows it with a voltage source and a voltmeter, with two loops (one of which has no current).

The potential energy is just , there is no kinetic energy (no inductors), and the dissipation is . Taking the derivatives of the Lagrangian gives us
and
.
In other words, we get the voltage at the voltage source and the voltage at the voltmeter. If we want to do anything with these equations, we need to recognize that the and terms are 0 (modeling the voltmeter as a perfect infinite impedance), giving us the usual formulas for the input and output voltage, in terms of the charge on the capacitor: and .

If we take Laplace transforms, we get and , which gives us the transfer function , as expected.  (Plug in to get the usual format in terms of angular frequency.)

I could do another, more complicated example, but I think that the idea is clear (to me):

• Make a charge (and current) coordinate for each current loop in the circuit—including a dummy loop with current 0 wherever you want to measure the voltage.
• Set up the Lagrangian by adding terms for each inductor (kinetic energy) and subtracting terms for each capacitor (potential energy), and set up the power-dissipation functions by adding terms for each resistor.
• Take the appropriate derivatives to get the voltages.
• If needed, eliminate charge terms by using more easily measured voltage terms.

I don’t find this process any simpler than using complex impedances and the usual Kirchhoff laws, but it isn’t much more complicated.  It may be easier to use the Lagrangian formulation than setting up the equations directly when there are mutual inductances to deal with—I’ll have to think about that some more.

Of course, the big advantage I’ve been told about for Lagrangian mechanics is in electromechanical systems, where you model the mechanical part as in Having trouble learning Lagrangian mechanics and the electronic part as in this post, with only a conservative coupling network added to combine the two. It is in setting up the coupling network that I get confused when trying to model electromechanical systems, and I’ll leave that confusion for a later post.

Having trouble learning Lagrangian mechanics

For the past few days, I’ve been trying to teach myself enough Lagrangian mechanics that I can derive systems of ordinary differential equations for the sorts of simple systems that come up in control-theory classes.

I think I’ve kind of got it for mechanical systems, and maybe for electronic ones, but I can’t seem to wrap my head around electromechanical systems.  I’m going to dump out a little of my understanding here, to clarify it in my own head, and to get corrections or suggestions from my readers, many of whom are far better at physics than me, having actually taken it in college. My son and I studied simple physics using the textbook Matter and Interactions a few years ago, but the book doesn’t get into Lagrangian mechanics, and I don’t think I really understand magnetic fields intuitively well enough to keep the mathematical abstractions straight.

Part of my problem in reading introductions to Lagrangian mechanics (like the Wikipedia one) is that they use almost impenetrable abstract notation and immediately jump to very general cases, leaving me with no intuition about what they are doing.

As I understand it, Lagrangian mechanics starts with the idea of a conserved scalar quantity (like energy), and provides a way of setting up equations of motion by taking partial derivatives with respect to generalized coordinates, which are in turn functions of time.

For mechanical systems the generalized coordinates are generally positions of point masses or angles of joints (velocity and angular velocity are time derivatives of the coordinates).  For electronic systems, the generalized coordinates are either charges or voltages and currents, depending whose formulation you read.  The charge-based formulation has made a bit more sense to me, as currents are the time-based derivatives of charge.  We look at the charge on capacitors and current through inductors to compute energy in the system.

One problem with a lot of the descriptions of Lagrangian mechanics is that they do everything with purely conservative systems, then tack in dissipation as an afterthought, but all real systems that need control have dissipation of energy as a fundamental part of the modeling process.  I’ll try to include the dissipation terms in the basic formulation, rather than adding them  at the end.

Some notation:

• is the difference between kinetic and potential energy of the system.  In a conservative system, it would always be 0, with energy sloshing back and forth between kinetic and potential forms, but never increasing or decreasing.Correction based on comments: I screwed up here—it is the sum of kinetic and potential energy (the Hamiltonian) not the difference (the Lagrangian) that is constant in a conservative system.
• is the power dissipated by the system.
• is the vector input to the system needed to make the energy balance work out.   The units for this vector depend on what the generalized coordinates are.  For mechanical systems, Cartesian coordinates will need forces, and angles will need torques.  For electronic systems using charges as coordinates, the units are volts.

With this notation, the basic formula is

I may be missing some critical conditions on when this can be applied, but I did manage to work out the equations of motion for an inverted pendulum on a cart from it.

So here is the inverted-pendulum example:

We have two coordinates: the horizontal position of the cart , and the angle of the inverted pendulum (clockwise from upright) .  The cart has mass and the pendulum , with a distance from the pivot on the cart to the center of  mass for the pendulum .  Furthermore, the pendulum has moment of inertia , and there is viscous drag on the cart with a force .  The pivot is assumed to be frictionless.

Let’s use to designate the location of the center of mass of the pendulum: .

The potential energy in the system is just due to the height of the pendulum mass: .  The kinetic energy is . Combining these gives us

The power dissipated due to friction is .

It would be good to get rid of the extra variable , using just and .  The derivative is , and its square is .  Substituting that into our previous formula gives us the Lagrangian in terms of just the generalized coordinates and their time derivatives:

Applying the basic formula gives us

We can linearize this around (the inverted pendulum straight up), by setting and , except for the gravitational term, where we use :

These equations of motion can be used to design a controller for the cart and inverted-pendulum system, as long as you don’t let the pendulum get too far from the vertical.  I think that the linearized equations are ok, but I may have made some calculus errors in the nonlinear equations I simplified them from.

I’ll stop here, but try to do another (electronic) example in a later blog post.

Battery connectors

I spent a little time today working on my book, but I got side tracked into a different project for the day: designing a super-cheap coin-cell battery connector. I’ve used coin-cell battery holders before, like on the blinky EKG board, where I used a BH800S for 2 20mm CR2032 lithium cells. That battery holder is fairly large and costs over $1—even in 1000s it costs 70¢ a piece. So I was trying to come up with a way to make a dirt cheap coin-cell holder.

The inspiration came from the little LED lights that “glovers” use inside their gloves. They are powered by two CR1620 batteries (that means a 16mm diameter and 2.0mm thickness for the battery). Because the lights have to be made very cheaply, they don’t use an expensive holder, but put the negative side of the batteries directly against a large copper pad on the PC board. The batteries are held in place by the positive contact, which is a piece of springy metal pressing the battery against the board—and each manufacturer seems to have a slightly different variant on how the clip is made.

Unfortunately, I was unable to find any suppliers who sold the little clips—though I found several companies that make battery contacts, it seems that most are custom orders.

My first thought was to bend a little clip out of some stainless steel wire I have sitting around (not the 1/8″ welding rod, but 18-gauge 1.02362mm wire). That’s about the same thickness as a paperclip (which is made out of either 18-gauge or 19-gauge wire), but the stainless steel is stiffer and less fatigue-prone than paperclips. I was a little worried about whether stainless steel was solderable, so I looked it up on Wikipedia, which has an article of solderability. Sure enough, stainless steel is very hard to solder (the chromium oxides have to be removed, and that takes some really nasty fluxes that you don’t want near your electronics). So scratch that idea.

I spent some time looking around the web at what materials do get used for battery contacts—it seems there are three main ones: music wire, phosphor bronze, and beryllium copper, roughly in order of price. Music wire is steel wire, which gets nickel plated for making electrical connections. It is cheap, stiff, and easily formed, but its conductivity is not so great, though the nickel plating helps with that. The nickel oxides that form require a sliding contact to scrape off to make good electrical connection. Phosphor bronze is a better conductor, but may need plating to avoid galvanic corrosion with the nickel-plated battery surfaces. Most of the contacts I saw on the glover lights seemed to have been stamped out of phosphor bronze. Beryllium copper is a premium material (used in military and medical devices), as it has a really good ratio of yield strength to Young’s modulus, so it can be cycled many times without failing, but also has good conductivity.

Since I don’t have metal stamping machinery in my house, but I do have pliers and vise-grips, I decided to see if I could design a clip out of wire. It is possible to order small quantities of nickel-plated music wire on the web. For example, pianoparts.com sells several different sizes, from 0.1524mm diameter to 0.6604mm diameter. I may even be able to get some locally at a music store.

My first design was entirely seat-of-the-pants guessing:

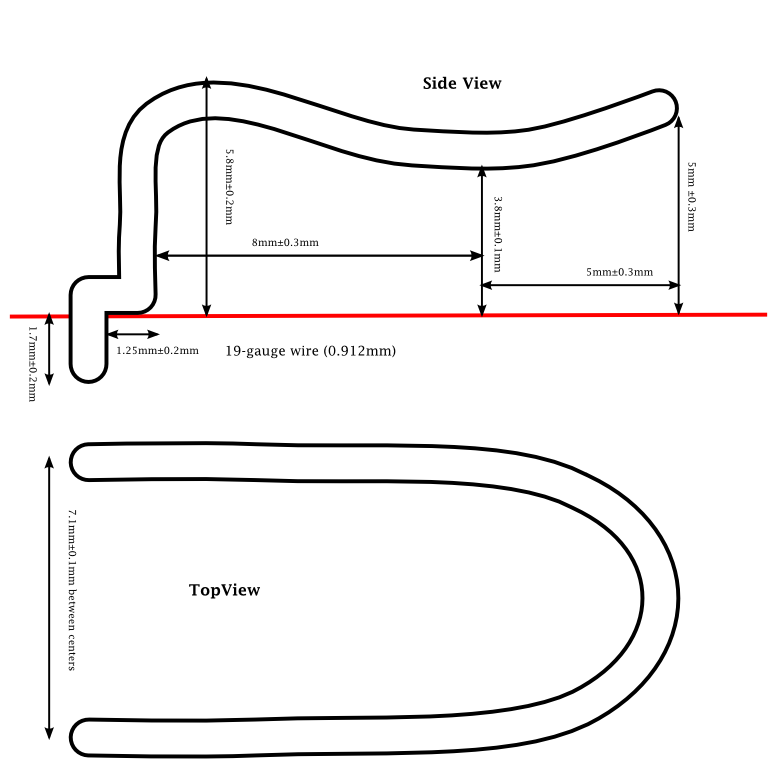
First clip design, using 19-gauge wire, with two 1mm holes in PC board to accept the wire. This design is intended for two CR1620 batteries.

The idea was to have a large sliding contact that made it fairly easy to slide the batteries in, but then held them snugly. Having a rounded contact on the clip avoids scratching the batteries but can (I hope) provide a fair amount of normal force to hold the batteries in place. But how much force is needed?

I had a very hard time finding specifications on how hard batteries should be held by their contacts. Eventually I found a data sheet for a coin battery holder that specified “Spring pressure: 50g min. initial contact force at positive and negative terminals”. Aside from referring to force as pressure and then using units of mass, this data sheet gave me a clear indication that I wanted at least 0.5N of force on my contacts.

I found another battery holder manufacturer that gave a tiny graph in one of their advertising blurbs that showed a range of 100g–250g (again using units of mass). This suggests 1N-2.5N of contact force.

Another way of getting at the force needed is to look at how much friction is needed to hold the batteries in place and what the coefficient of friction is for nickel-on-nickel sliding. The most violently I would shake something is how fast I can shake my fingertips with a loose wrist—about 4Hz with an peak-to-peak amplitude of 22cm, which would be a peak acceleration of about 70 m/s^2. Two CR1620 cells weigh about 2.5±0.1g (based on different estimates from the web), so the force they need to resist is only about 0.2N. Nickel-on-nickel friction can have a coefficient as low as 0.53 (from the Engineering Toolbox), so I’d want a normal force of at least 0.4N. That’s in the same ballpark as the information I got from the battery holder specs.

So how stiff does the wire have to be? I specified a 0.2mm deflection, so I’d need at least 2N/mm as the spring constant for the contact, and I might want as high as 10N/mm for a really firm hold on the batteries.

So how should I compute the stiffness of the contact? I’ve never done mechanical engineering, and never had a statics class, but I can Google formulas like any one else—I found a formula for the bending of a cantilever loaded at the end:
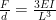, where F is force, d is deflection, E is Young’s modulus, I is “area moment of inertia”, and L is the length of the beam. More Googling got me the area moment of inertia of a circular beam of radius r as . So if I use the 0.912mm wire with an 8mm beam I have
F/d = 200E-6 mm E.

More Googling got me some typical values of Young’s modulus:

material	E [MPa = N/(mm)^2]
phosphor bronze	120E3
beryllium copper	135E3
music wire	207E3

If I used 19-gauge phosphor bronze, I’d have about 24N/mm, which is way more than my highest desired value of 10N/mm. Working backwards from 2–10N/mm what wire gauge would I need? I get a diameter of 0.403mm to 0.603mm, which would be #6 (0.4064mm), #7 (0.4572mm), #8 (0.5080mm), #9 (0.5588mm), or #10 (0.6096mm), on the pianoparts.com site. I noticed that battery contact maker in Georgia claims to stock 0.5mm and 0.6mm music wire for making battery contacts, though they first give the sizes as 0.020″ and 0.024″, so I think that these are actually 0.5080mm and 0.6096mm (#8 and #10) music wire.

It seems that using #8 (0.020″, 0.5080mm) nickel-plated music wire would be an appropriate material for making the contacts. Note that the loop design actually results in two cantilevers, each with a stiffness of about 4N/mm, resulting in a retention force of about 1.6N. The design could be tweaked to get different contact forces, by changing how much deflection is needed to accommodate the batteries.

How much tweaking might be needed?  I found the official specs for battery sizes (with tolerances) in IEC standard 60086 part 2: The thickness for a 1620 is 1.8mm–2mm, the diameter is 15.7mm–16mm, and the negative contact must be at least 5mm in diameter.  The standard also calls for them to take an average of 675 hours to discharge down to 2v through a 30kΩ resistor (that’s about 56mAH, if the voltage drops linearly, 67mAH if the voltage drops suddenly at the end of the discharge time).  If the batteries can legally be as thin as 1.8mm, then to get a displacement of 0.2mm, I’d need the zero-point for the contacts to be only 3.4mm from the PC board, not 3.8mm, and full thickness batteries would provide a displacement of 0.6mm, and a retention force of about 4.8N.

If I were to do a clip for a single CR2032 battery, I’d need to have a zero-point 2.8mm from the board, to provide 0.2mm of displacement for the minimum 3.0mm battery thickness.

So now all I need to do is get some music wire and see if I can bend it by hand precisely enough to make prototype clips.  I’d probably change the spacing between the holes to be 0.3″ (7.62mm), so that I could test the clip on one of my existing PC boards.

Update 2014 July 6: I need to put an insulator on the verticals (heat shrink tubing?), or the top battery will be shorted out, since the side of the lower battery is exposed.

 

Establishing the habit of writing

In Preparing for AP Physics 1: establishing the habit of writing Greg Jacobs writes

I’m in the infant stages of planning my AP Physics 1 course. The big trick is going to be establishing my students’ ability and willingness to write their reasoning, to get them to focus on communication rather than on getting a correct numerical answer. Once it’s clear that they are not taking a math course—once they see that the solution to a problem looks much more like what they’ve done in biology or economics than in calculus—I think the students will be able to move along quickly and enthusiastically through the material.

Students must get comfortable with calculation. However—as was correctly pointed out to me at the AP consultant meeting in April—if we start the course with lots of pure calculation, students will think that getting the answer is the holy grail of physics problems. If instead we begin the course demanding description, explanation, and all sorts of prose, students may become accepting of the idea that a numerical answer is merely the result of careful reasoning.

If this change in AP Physics actually works (something I’m always skeptical about in any curriculum reform, particularly at the high school level), it may help engineering students in college. Engineers do far more writing than most professions, with far less training at doing it.

I don’t think that a prompt that just says “In a clear, coherent, paragraph-length explanation, describe how you would figure out …” is going to do the trick, though. If they could already write clear, coherent paragraphs about how they would figure something out, then they would not need the curriculum change—they might not even need a physics class at the level of Physics 1.

I’m struggling with this problem in my applied circuits course, in which I require weekly design reports for the circuits they design and build. The students are staying in lab until they finish the designs and demo them, so they are clearly capable of doing the work (though not always as quickly as they should). But only a few students can explain their computations for the design parameters (like gain, corner frequency, and component values) clearly—others put down any nonsense that has a few of the right buzzwords in it.

The top students have gotten better at their explanations as a result of feedback, but the bottom students are still often producing word salad. Although there is some indication of a general writing problem (lack of topic sentences, poor grammar, and misused vocabulary), the problem is most pronounced when they are trying to explain how they selected component values. The more steps that there are in the underlying math, the more jumbled their explanations, even if the problem is just a chain of multiplications.

From time to time, I’ve suspected that the students don’t produce coherent sentences about how they computed something may not have actually done the computation, but “borrowed” the result.  This is not an explanation I believe in strongly, though, as the students have been (mostly) coming up with different solutions to the design tasks, so there isn’t simple copying going on. I’ve also seen the design process the students use, as they have been doing their pre-lab work in lab (instead of at home), so I hear them discussing the problems.  They do ask each other not just what answer they got, but how to get the answers, so they are trying to learn the method.

In looking at the pre-lab homeworks that were turned in on Monday I realized what part of the problem is—the students keep absolutely awful design notes. What the students turned in on Monday (even the top students) was mostly incomprehensible scribbling of numbers, with no indication where the numbers come from or what they were attempting to compute.  Half an hour after writing down the notes, I’m pretty sure that they could not reconstruct their reasoning—hence the often magical methods in their design reports, where they copy numbers out of their notes (some of which are correct), but can’t put together a coherent chain of reasoning that leads to those numbers. On the long multi-step computations needed to figure out what gain an amplifier needs, they can usually do each step (though often needing coaching on one or two of the steps, either by me or by one of the better students in the course), but they don’t record the meaning of each step or even what the sequence of steps is, and the “answer-getting” mentality causes them to flush the process from their minds as soon as they have a number.

I’ve seen a lot of lab exercises for other courses that try to scaffold the process by providing worksheets that give the step-by-step process and have the students fill it out as they go along. I don’t think that this is helpful though, as it encourages students to solve one step at a time and then forget about it—the scaffold prevents the students from exercising the very skill that I most need them to learn. Showing them worked examples, as I have done in class, doesn’t seem to help much either—they can follow along as I break the problem down with them, and think they understand, but then not be able to do the same thing themselves.  Again, the scaffolding prevents them from exercising the skill I most need them to learn—identifying problems and them into subproblems.

For next year, I’m probably going to have to come up with some exercises which get students to organize their thoughts external to their heads. So far, the only thing I’ve thought of is to have them create a fill-in-the-blank worksheet for each lab (like an income tax form), and turn in the blank worksheet and try filling out each other’s worksheets.  If they get in the habit of writing down the steps as steps, it may help them be able to reconstruct their work when they convert it into full sentences for the final reports. It may be too late for me to do anything formal this year (only 2.5 weeks left), but I’ll suggest it to the students anyway.

The advice I’d give to Greg Jacobs is to leave the “clear, coherent paragraph” until later in the quarter—get them to create worksheets first.

I’d welcome any suggestions from my blog readers on ways that I can get students to learn to organize their thoughts in a way that they can present them coherently to others. Block diagrams alone don’t seem to be enough, and vague things like “mind maps” are likely to do more harm than good.