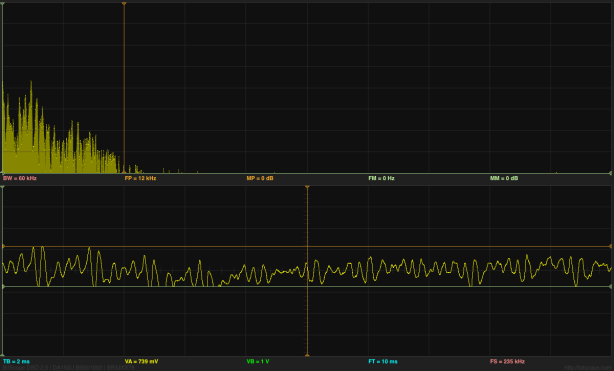
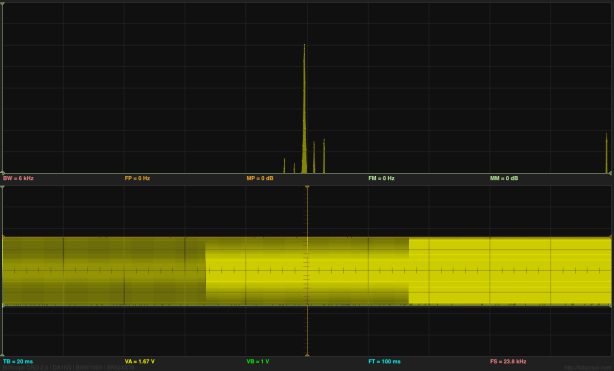
In Dehumidifier, I provided spectral analysis of the sound from the 30-pint Whynter RPD-321EW Energy Star Portable Dehumidifier, using my BitScope USB oscilloscope to record the sound and averaging the absolute value of the FFT over 100 short traces. Today I decided to improve the FFT analysis by using the scipy.signal.welch() function to split a longer trace into windows, apply a Dolph-Chebyshev window-shaping function, and average the resulting power spectra. The main improvement here is the use of the window-shaping function.
I used PteroDAQ with a Teensy LC board to record at 15kHz, which was as fast as I could go with 4× averaging communicating with my old MacBook Pro laptop. Based on the Bitscope recordings, though, that should include all the interesting signal, which appears to be limited to about 5.4kHz. I could only record for about 330,000 samples to avoid overrunning the USB buffer and dropping samples, so I also tried 12kHz, which allowed me to run longer. The analysis looked much the same, with no apparent reduction in the noise floor, so I’ll only present the 15kHz results. (Note: when I get a new laptop this fall, I should be able to run at this sampling rate for much longer, which should allow smoothing out more of the noise.)

The dehumidifier looks very much like 1/f noise, with a big spike around 1050Hz. The spikes at 60Hz, 120Hz, 240Hz, and 360Hz may be electrical noise picked up by the sound amplifier, rather than acoustic noise.
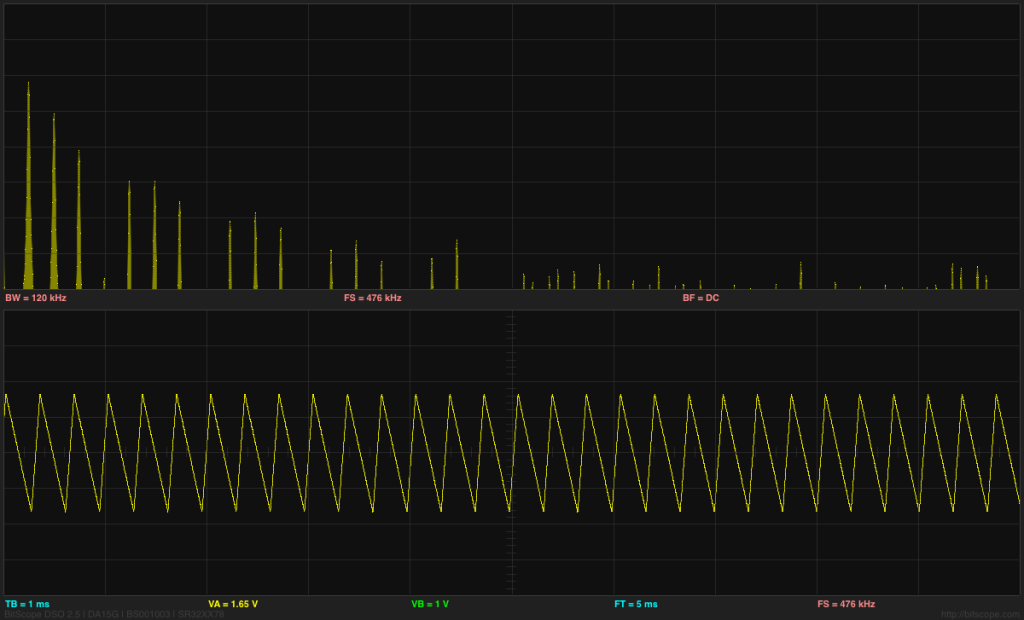
Using Welch’s method and a proper window function results in a much cleaner spectrum than before. I used a 216 FFT window for the analysis, since I had plenty of data, which gives a fairly fine resolution of about 0.23Hz. The 60Hz spike is appearing at 58.36Hz, which is a little troubling, as the PteroDAQ crystal and the power company both have better frequency control than a 2.7% error. The 120Hz, 240Hz, and 360Hz spikes are at most one bin off from where they should be, so I don’t understand the shift at 60Hz.
I checked my code by testing with a recording of a triangle wave, and found that Welch’s method with an 80dB Dolph-Chebyshev window did an excellent job of removing the spectral smear that I was getting by just averaging rectangular FFT windows (my first approach). The noise floor for Welch’s method on those measurements was pretty much flat across the entire spectrum (maybe rising at higher frequencies), so the 1/f plot here is not an artifact of the analysis, but a real measurement of the acoustic noise. Using 60dB window resulted in a higher noise floor, but 100dB and larger did not lower the noise floor, so I stuck with 80dB as a good parameter value. It might be useful to use other values if the FFT window width is changed or the noise in the data is different.
I’ve included the source code for the program, so that others can use it. It does require that SciPy be installed, in order to use the scipy.signal package.
#! /usr/bin/env python3
"""Sun Sep 4 21:40:28 PDT 2016 Kevin Karplus
Reads from stdin a white-space separated file
whose first column is a timestamp (in seconds) and
whose subsequent columns are floating-point data values.
May contain multiple traces, separated by blank lines.
Outputs a tab-separated file with two columns:
the frequencies
the Fourier transform
"""
from __future__ import print_function, division
import argparse
import sys
from math import sqrt
import numpy as np
try:
from future_builtins import zip
except ImportError: # either before Python2.6 or one of the Python 3.*
try:
from itertools import izip as zip
except ImportError: # not an early Python, so must be Python 3.*
pass
import scipy
import scipy.signal
class Trace:
"""One contiguous trace consisting of two 1D numpy arrays of the same length
times: timestamps in seconds
values: arbitrary floats
and sampling_freq: the sampling frequency in Hz
"""
def __init__(self,times,values,sampling_freq=None):
self.times=np.array(times)
self.values=np.array(values)
assert self.times.shape==self.values.shape
if sampling_freq is None and len(times)>1:
sampling_freq = (len(times)-1)/(times[-1]-times[0])
self.sampling_freq=sampling_freq
def __len__(self):
return len(self.values)
def read_trace(file, column=2, sampling_freq=None, echo_comments_to=None):
"""Generator that yields traces from tab-separated rows of data.
Each row contains a timestamp in the first column and any number of subsequent
columns, one of which is selected to be the values for the trace.
New traces are started whenever the timestamp in the first column decreases.
If sampling_freq is None, the sampling_freq for the
trace is deduced from the timestamps.
Comments and blank lines are echoed to a file-like object,
echo_comments_to, if it is not None.
"""
times=[] # time values (in seconds) from frst column
values=[] # values from the specified column
for line in file:
line=line.strip()
if line.startswith('#') or len(line)==0:
if echo_comments_to is not None:
print(line, file=echo_comments_to)
continue
fields=line.split()
if len(fields)>=column:
time=float(fields[0])
if times and time<times[-1]:
yield Trace(times=times, values=values, sampling_freq=sampling_freq)
times=[]
values=[]
times.append(time)
values.append(float(fields[column-1]))
if times:
yield Trace(times=times, values=values, sampling_freq=sampling_freq)
def posint(opt):
"""returns int(opt) if that is positive,
otherwise raises an argparse.ArgumentTypeError
"""
try:
x = int(opt)
except:
x=None
if x is None or x<=0:
raise argparse.ArgumentTypeError("{} is not a positive integer".format(opt))
return x
def parse_options(argv):
"""Parse the options and return what argparse does:
a structure whose fields are the possible options
"""
parser = argparse.ArgumentParser( description= __doc__, formatter_class = argparse.ArgumentDefaultsHelpFormatter )
parser.add_argument("--sampling_freq","-s", type=float,
default=None,
help="""Sampling frequency (in Hz).
If none specified, then estimate sampling frequency from the timestamps.
""")
parser.add_argument("--window", "-w", type=posint,
default=(1<<16),
help="""Max window size (in samples) for FFT.
Longer traces will be split up into windows of this size
""")
parser.add_argument("--column" , "-c", type=posint, default=2,
help="""What column should be Fourier transformed?""")
parser.add_argument("--welch" , type=float, default=None,
help="""Use Welch's method to produce averaged spectrum from windows.
Value is dB difference between main lobe and sidelobes for Dolph-Chebyshev window.
80 seems reasonable with 16-bit data (60 produces a higher noise floor, without noticeably narrowing the spikes).
Note, sqrt is used to get amplitude spectrum, rather than power spectrum. """)
options=parser.parse_args(argv[1:])
return options
def main(argv):
"""parse the command line arguments and do FFTs
"""
options = parse_options(argv)
sampling_freq= options.sampling_freq
# input file may contain separate time traces.
# Each new trace stats when the time value is less than the previous time.
for trace in read_trace(sys.stdin, column=options.column,
sampling_freq=options.sampling_freq,
echo_comments_to=sys.stdout):
print("# using sampling frequency {:.6f} Hz for FFT of trace with {} samples".format(trace.sampling_freq,len(trace)))
fft_len=64 # length of the fft to do
while fft_len<len(trace) and fft_len<options.window:
fft_len *= 2
if options.welch is not None:
welch_f,welch_spectrum = scipy.signal.welch(trace.values, trace.sampling_freq, nperseg=fft_len, scaling="spectrum", window=("chebwin",options.welch))
print("") # separate the traces
for f,w in zip(welch_f,welch_spectrum):
print("{0:.7f}\t{1:.6f}".format(f, sqrt(w)*(fft_len//2)))
else:
for start in range(0,len(trace),fft_len):
window=trace.values[start:start+fft_len]
# remove DC component, so that zero-padding makes sense
# WARNING: This in-place change could introduce errors if
# overlapping windows are allowed.
dc = sum(window)/len(window)
window -= dc
fft = scipy.fftpack.fft(window, n=fft_len)
fft[0] += dc
print("") # separate the traces
print("# Window width {} = {:.3f}s".format(fft_len,fft_len/trace.sampling_freq))
for i,f in enumerate(fft[0:fft_len//2]):
print("{0:.7f}\t{1:.6f}".format(i*trace.sampling_freq/fft_len, f))
if __name__ == "__main__" :
sys.exit(main(sys.argv))